Calcolatore di deviazione standard

Enter Inputs	5,20,40,80,100 Enter the Numbers with Comma separated(,)

Result:
No.of Inputs
Mean
Standard Deviation(SD)
Population Standard Deviation(PSD)
Variance(SD)
Variance(PSD)
Calculation

Il calcolatore di deviazione standard per calcolare la misura comune della diffusione di un set di dati, è un'analisi dei dati. La calcolatrice potrebbe darti ingressi, media, deviazione standard (SD) (SD), deviazione standard della popolazione (PSD), varianza (SD), varianza (PSD) di un determinato valori di input del set di dati.

Formula di deviazione standard

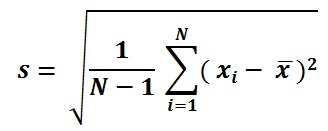
Standard Deviation Formula & Calculation

Popolazione SD Formula.

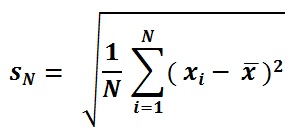
PSD - Population Standard Deviation Formula & Calculation

Formula della varianza

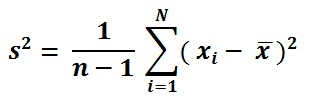
Variance Formula & Calculation

Formula media

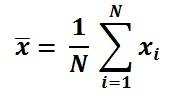
Mean Formula & Calculation

Ad esempio, quando è stato dato un set di dati 5,20,40,80,100 , il risultato sarà:

.

Ingressi totali (n) = (5,20,40,80,100)

Ingressi totali (n) = 5

Media (xm) = (x1 + x2 + x3 ... xn) / n

Media (XM) = 245/5

Significa (xm) = 49

-------------------------------------------

Sd =.

SQRT (1 / (N-1) * ((X1-XM) ^ 2 + (X2-XM) ^ 2 + .. + (XN-XM) ^ 2))

= SQRT (1 / (5-1) ((5-49) ^ 2 + (20-49) ^ 2 + (40-49) ^ 2 + (80-49) ^ 2 + (100-49) ^ 2 ))

= SQRT (1/4 (((- 44) ^ 2 + (- 29) ^ 2 + (- 9) ^ 2 + (31) ^ 2 + (51) ^ 2))

= SQRT (1/4 ((1936) + (841) + (81) + (961) + (2601)))

= SQRT (1605)

= 40.0625.

Varianza = SD ^ 2

Varianza = 40.0625 ^ 2

Varianza = 1605.

-------------------------------------------

PSD =.

SQRT (1 / (N) * ((X1-XM) ^ 2 + (X2-XM) ^ 2 + .. + (XN-XM) ^ 2))

= SQRT (1 / (5) ((5-49) ^ 2 + (20-49) ^ 2 + (40-49) ^ 2 + (80-49) ^ 2 + (100-49) ^ 2))

= SQRT (1/5 (((- 44) ^ 2 + (- 29) ^ 2 + (- 9) ^ 2 + (31) ^ 2 + (51) ^ 2))

= SQRT (1/5 ((1936) + (841) + (81) + (961) + (2601)))

= SQRT (1284)

= 35.8329.

Varianza = SD ^ 2

Varianza = 35.8329 ^ 2

Varianza = 1284.

Calcolatore di deviazione standard

FoxCalculators - Calcolatrici gratuite online!