Calcolatore di errore standard |
| Result: | |
Il calcolatore di errore standard per calcolare il metodo di misurazione o errore standard.
Formula standard di errore
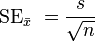
dove
n è la dimensione (numero di osservazioni) del campione.
S è la deviazione standard del campione.
Ad esempio, quando il set di dati è {5,20,40,80,100}
.Ingressi totali (n) = (5,20,40,80,100)
Ingressi totali (n) = 5
Media (xm) = (x1 + x2 + x3 ... xn) / n
Media (XM) = 245/5
Significa (xm) = 49
-------------------------------------------
Sd =.
SQRT (1 / (N-1) * ((X1-XM) ^ 2 + (X2-XM) ^ 2 + .. + (XN-XM) ^ 2))
= SQRT (1 / (5-1) ((5-49) ^ 2 + (20-49) ^ 2 + (40-49) ^ 2 + (80-49) ^ 2 + (100-49) ^ 2 ))
= SQRT (1/4 (((- 44) ^ 2 + (- 29) ^ 2 + (- 9) ^ 2 + (31) ^ 2 + (51) ^ 2))
= SQRT (1/4 ((1936) + (841) + (81) + (961) + (2601)))
= SQRT (1605)
= 40.06245124802026.
-------------------------------------------
Trovare errori standard
Errore standard = SD / SQRT (N)
Errore standard = 40.06245124802026 / SQRT (5)
Errore standard = 40.0625 / 2.2361
Errore standard = 17.9165
seleziona lingua:日本語 | 한국어 | Français | Español | ไทย| عربي | русский язык | Português | Deutsch| Italiano | Ελληνικά | Nederlands | Polskie| Tiếng Việt| বাংলা| Indonesia| Pilipino| Türk| فارسی| ລາວ| ဗမာ| български| Català| čeština| Қазақ| Magyar| Română| Україна
Copyright ©2021 - 2031 All Rights Reserved.