Eigenvettori e calcolo degli autovalori

Regular Matrix A =
Identity Matrix I =
Scalar Matrix(Z=c×I)
c =
|A| =
Singular Matrix (A - c×I) =
|A - c×I| =
Trace of A =
Eigen Value (c2) =
Eigen Value (c1) =
c1 in Eigen Vector x1 value =
c2 in Eigen Vector x1 value =
c1 in Eigen Vector x2 value =
c2 in Eigen Vector x2 value =

Un eigenvettore di una matrice quadrata A è un vettore diverso da zero V, quando una V = λ V, la λ è chiamata eigenvalore di un corrispondente a V.

Tutti gli autovalori e gli eigenvettori soddisfano l'equazione AX = λx per una data matrice quadrata A.

Gli eigenvettori online e il calcolatore Eigenvalues ​​possono ottenere | A |, singolare matrice (A - C × I), traccia di A, Eigen Valore della matrice A

Per esempio

Per Matrix.

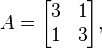
il vettore.

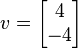
è un eigenvector con eigenvalue 2.

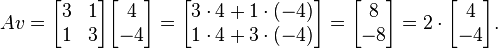
D'altra parte il vettore

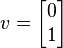
è non un eigenvector, poiché

.

.

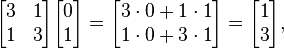
E questo vettore non è un multiplo del vettore originale v.

Eigenvettori e calcolo degli autovalori
Calcolatori di raccomandazioni La legge di Ohm con corrente, resistenza e calcolatrice di potenza Calcolatrice della legge di Ohm KVA, KW, conversione KVA Calcolatore del resistore limitante corrente a LED Calcolatore di frequenza del circuito RLC Calcolatrice IC 555 Timer (modalità monostabile e astabile) Calcolatore di guadagno elettronico Calcolatore di induttanza della bobina a strato singolo Calcolatore del registro UART MSP430 Calcolatore della bobina a strato singolo Calcolatore del codice colore con condensatore in poliestere Calcolatore del resistore OP-AMP non invertente Calcolatore del resistore della serie LED Calcolatore della durata della batteria Calcolatore del resistore limitante della corrente del LED parallelo