FoxCalculators - Calcolatrici gratuite online!

Un eigenvettore di una matrice quadrata A è un vettore non zero V che, quando la matrice viene moltiplicata per V, produce un multiplo costante di V, il moltiplicatore viene denotato comunemente da λ. Cioè: a v = λ v

(Poiché questa equazione utilizza post-moltiplicazione da V, descrive un eigenvettore destro.) Il numero λ è chiamato EigenValue di un corrispondente a V.

Tutti gli autovalori e gli eigenvettori soddisfano l'equazione AX = λx per una data matrice quadrata A.

Semplice matrice calcolatrice per calcolare il valore di Eigen e il vettore Eigen di una matrice 3x3. Immettere i valori della matrice 3x3 e fare clic sul pulsante Calcola.

Traccia

La traccia, tr (a) di una matrice quadrata A è la somma delle sue voci diagonali. Mentre la moltiplicazione della matrice non è commutativa come menzionato sopra, la traccia del prodotto di due matrici è indipendente dall'ordine dei fattori:

tr (ab) = tr (ba).

Questo è immediato dalla definizione di moltiplicazione della matrice:

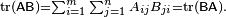
Inoltre, la traccia di una matrice è uguale a quella della sua trasposizione, cioè.

tr (a) = tr (a ^{T ).}