Equazione cartesiana di un calcolatore aereo

Point A , ,
Point B , ,
Point C , ,
   
Equation of the plane
(given three points)		 x+y+z+=0

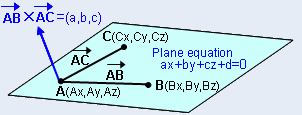
Ci sono tre punti A (x 1 , y 1 , z 1 ), b (x 2 , y 2 , z 2 ) e c (x 3 , y 3 , z 3 ) Sdraiato su un aereo, quindi l'equazione del piano può essere trovata usando la seguente formula

.

.

.

.

x - x 1

y - y 1

Z - Z 1

= 0

x 2 - x 1

y 2 - y 1

z 2 - z 1

x 3 - x 1

y 3 - y 1

Z 3 - z 1

O A (AX, AY, AZ), B (BX, BY BZ), C (CX, CY, CZ), l'equazione del piano è AX + BY + CZ + D = 0

Dove,

A = (by-ay) (CZ-AZ) - (CY-AY) (BZ-AZ)

B = (BZ-AZ) (CX-AX) - (CZ-AZ) (BX-AX)

c = (bx-ax) (cy-ay) - (cx-ax) (by-ay)

D = - (Aax + Bay + Caz).

Il calcolo dell'equazione del piano cartesiano con le tre coordinate è reso più facile qui.

Equazione cartesiana di un calcolatore aereo
Calcolatori di raccomandazioni La legge di Ohm con corrente, resistenza e calcolatrice di potenza Calcolatrice della legge di Ohm KVA, KW, conversione KVA Calcolatore del resistore limitante corrente a LED Calcolatore di frequenza del circuito RLC Calcolatrice IC 555 Timer (modalità monostabile e astabile) Calcolatore di guadagno elettronico Calcolatore di induttanza della bobina a strato singolo Calcolatore del registro UART MSP430 Calcolatore della bobina a strato singolo Calcolatore del codice colore con condensatore in poliestere Calcolatore del resistore OP-AMP non invertente Calcolatore del resistore della serie LED Calcolatore della durata della batteria Calcolatore del resistore limitante della corrente del LED parallelo